A Brief History of Algorithmic Stablecoins Bursting into Action or Dying in Silence?

Author: Solaire, YBB Capital

Introduction

Stablecoins have always been a crucial part of the crypto world, accounting for 8.6% of the total market value of the blockchain (approximately $124.5 billion). Centralized stablecoins collateralized by the US dollar and US Treasury bonds, such as USDT and USDC, have dominated the market. However, centralized stablecoins are always subject to central control. For example, Tether has the ability to freeze USDT in any address, and their security is guaranteed by centralized entities. This clearly contradicts the original intention of blockchain. In the exploration of decentralized stablecoins, two main branches have emerged: over-collateralized stablecoins and algorithmic stablecoins. Although over-collateralized stablecoins can maintain stability in a highly volatile crypto market due to their high collateralization rate, their low capital efficiency is caused by a minimum collateralization ratio of 1.5-2 times. On the other hand, the market for algorithmic stablecoins has always been the most ruthless. Although they have the highest capital efficiency, their model of close to zero collateralization always leads to their demise. After the failure of LUNA, this track has disappeared for a long time. However, the author has always believed that there should be a decentralized stablecoin without over-collateralization in the crypto world, and this article will explore the history of algorithmic stablecoins and some new ideas.

What are algorithmic stablecoins?

Generally speaking, algorithmic stablecoins are stablecoins that do not require any reserves or collateral. They completely regulate their supply and circulation through algorithms. This algorithm controls the supply and demand of the currency, aiming to peg the price of the stablecoin to a reference currency (usually the US dollar). Generally, when the price rises, the algorithm will issue more coins, and when the price falls, it will repurchase more coins from the market. This mechanism is similar to seigniorage, which is the way central banks regulate the supply and value of currency by issuing or destroying it. For some algorithmic stablecoins, their functions can be modified based on community suggestions, and this modification is achieved through decentralized governance, so the power of seigniorage is handed over to the users of the currency, not the central bank.

In summary, compared to common stablecoins like USDT and USDC, algorithmic stablecoins are different in terms of decentralization. They do not require reserves and are independent. Since algorithmic stablecoins are currencies based on the intrinsic relationship between mathematics, monetary economics, and technology, they introduce a stablecoin model that may be more advanced than centralized stablecoins.

A Brief History of Algorithmic Stablecoins

Early attempts that influenced later algorithmic stablecoins can be traced back to 2014 when economist Robert Sams proposed a model called “Seigniorage Shares”, which maintains price stability by automatically adjusting the money supply. This idea was somewhat inspired by modern central bank monetary policies. Next, BitShares attempted to adopt a hybrid model, which, although primarily based on asset collateralization, also included elements of algorithmic adjustments. This can be seen as an important step in the development of algorithmic stablecoins, although it is not a purely algorithmic stablecoin in itself.

In 2017, a project called Basis (formerly Basecoin) garnered wide attention. The project attempted to maintain the value of stablecoins through a complex three-token system. However, due to incompatibility with U.S. securities laws, the project was eventually forced to shut down at the end of 2018.

In 2019, Ampleforth proposed a new model called “elastic supply,” which not only adjusts the issuance of new tokens but also adjusts the quantity of existing tokens in users’ wallets to achieve price stability. Around the same time, Terra also released its stablecoin, which uses a composite model including taxation, algorithmic adjustments, and asset collateralization, minted through its native token. Of course, this token is also widely known as LUNA.

Terra LUNA

LUNA, as one of the most representative projects in algorithmic stablecoins, is also one of the most notorious projects in the crypto world. Its history is like a flash grenade, shining brightly in an instant and disappearing in the next. Today’s re-exploration of LUNA is just an attempt to learn from history and discover some insights for the future.

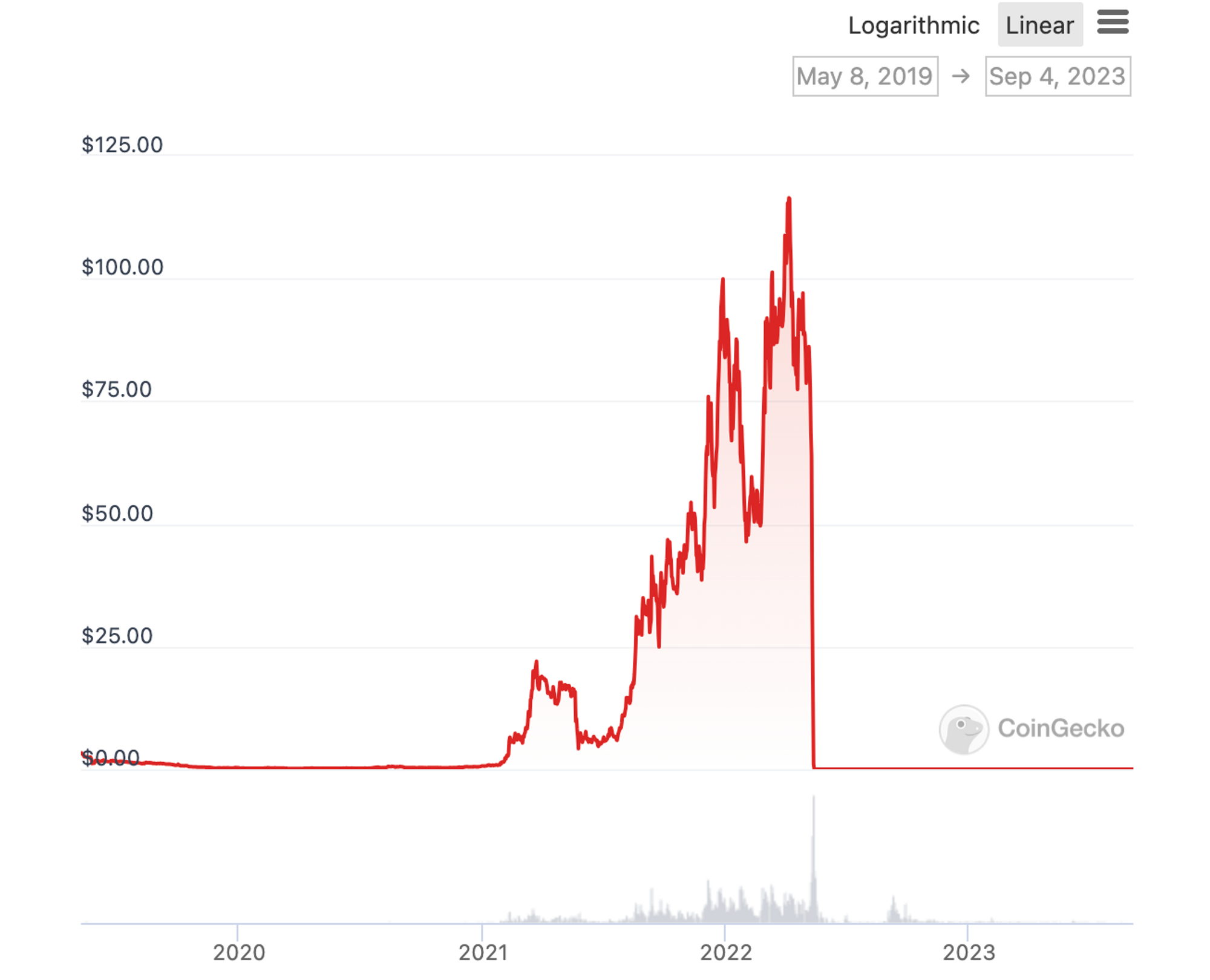
LUNA Historical K-Line (Data Source: CoinGecko)

Terra is a blockchain built on Cosmos SDK and Tendermint consensus, initially aimed at solving payment issues in e-commerce through cryptocurrency. However, traditional cryptocurrencies are too volatile to be used like fiat currencies, and centralized stablecoins like USDT have regional and centralization issues. Therefore, Terra wants to create a rich and decentralized portfolio of stablecoins, such as Korean won, Thai baht, and U.S. dollar.

To achieve this goal, Terra needs to launch a universal minting mechanism. Soon after, on a certain day in April 2019, a minting method was proposed by Terra’s co-founders Do Kwon and Daniel Shin in the whitepaper of Terra Money, which uses LUNA (Terra’s native token) to mint stablecoins of various countries. Let me briefly explain this method using UST (Terra’s U.S. dollar stablecoin) as an example.

– First, UST is pegged 1:1 to the U.S. dollar;

– If UST exceeds the pegged price, you can convert 1 U.S. dollar worth of LUNA into 1 UST. At this time, the value of UST exceeds 1 U.S. dollar, and you can earn the price difference by selling it;

– Conversely, if UST falls below the pegged price, you can always exchange 1 UST for 1 U.S. dollar worth of LUNA.

Since its launch, this model has faced constant scrutiny. From the birth of LUNA to its downfall, various well-known figures in the crypto community have warned that LUNA is nothing more than a Ponzi scheme. But despite this, many people continue to flock to this dangerous territory. So why is that?

Seigniorage

To understand a Ponzi scheme, one must first understand the motivation behind the scheme, which, in the case of UST’s widespread adoption, includes a crucial benefit—seigniorage.

Seigniorage is an economic concept that describes the revenue gained by governments through issuing currency. Specifically, this term is often used to refer to the difference between the face value of the currency and its production cost. For example, if the cost of producing a $1 coin is 50 cents, then the seigniorage is 50 cents.

In the crypto world, all three types of stablecoins have seigniorage. Stablecoins collateralized by fiat currencies generally charge a seigniorage fee of about 0.1% during the minting and burning process. Overcollateralized stablecoins generate revenue from transaction fees and interest paid by holders. As for algorithmic stablecoins, they have the highest seigniorage rate. By introducing a mechanism tied to a volatile token, stablecoins can convert all funds entering the system into seigniorage, which is essentially creating something out of nothing. This mechanism significantly reduces startup costs and to some extent improves the anchoring speed, but it also comes with inherent vulnerabilities.

Anchor Protocol

LUNA is a miracle in the history of algorithmic stablecoins. Prior algorithmic stablecoin projects either failed within a very short period of time or never managed to grow. LUNA not only secured the third position in the stablecoin sector but also became one of the few companies to bridge the gap in payment services.

Before Terra’s collapse, it had actually built an excellent financial ecosystem, including two payment systems built on the Terra protocol, CHAI and MemaLianGuaiy. CHAI had even seamlessly integrated with South Korea’s domestic payment channels and had partnerships with numerous businesses, including Nike Korea and Philips. Within Terra’s financial ecosystem, there were also active protocols for stocks, insurance, asset splitting, and more. In fact, Terra had already achieved great success in bringing the advantages of blockchain into the real world.

Unfortunately, all this prosperity was built on top of Do Kwon’s scam, rather than steadily advancing various use cases for UST. Do Kwon pressed the accelerator button with the Anchor Protocol, accelerating both Terra’s success and its demise.

Anchor Protocol is a decentralized bank within the Terra ecosystem that offers a very appealing savings product: a 20% APY risk-free UST deposit service (originally designed as 3% APY, but Do Kwon insisted on 20%). In a world where traditional banks cannot even provide a 1% interest rate, UST offers a 20% APY. Thus, Do Kwon found the mysterious button for massive UST minting and stablecoin dumping.

To maintain this scam, Do Kwon also became increasingly desperate in the later stages of Terra, resorting to refinancing and purchasing BTC to maintain UST’s annualized rate (there was a proposal to reduce the annualized rate to 4%, but Do Kwon knew that massive selling pressure was even more terrifying) and stability. However, paper can only cover up the fire for so long. On the night when UST migrated from Curve 3Pool to DAI killing 4Pool, when UST liquidity was at its lowest, a carefully planned short attack directly caused UST to decouple. Even BTC, serving as the second-line shield, failed to protect UST’s fixed exchange rate and instead fed the short attackers. At that moment, the giant empire of Terra collapsed instantly.

Parallel Worlds

If there were other parallel worlds, Do Kwon would not have pressed that button out of self-interest, nor would Terra have been attacked on the night of the UST migration pool. Can Terra avoid the fate of death in the end? The answer is no. In the parallel world where UST was not attacked, UST would still eventually die due to the death of the parasitic. Even without the parasitic, UST would still die due to forced pegging. Pegging another currency itself is extremely difficult, and even without encountering short selling attacks, it would still be crushed by many uncontrollable events due to its fragility.

Schwarzschild Radius

The Schwarzschild radius is a physical parameter on celestial bodies, which refers to the inevitable collapse into a black hole when any celestial body is smaller than its Schwarzschild radius.

In fact, this principle applies not only to celestial bodies, but also to algorithmic stablecoins like LUNA, and even to centralized stablecoins that adopt a “gold standard”. Since LUNA and UST are twin relationships, each of them is the Schwarzschild radius of the other. Once UST is decoupled or LUNA experiences liquidity problems while the minting mechanism is still running as usual, they will eventually collapse into “black holes” at a high speed.

As for centralized stablecoins collateralized by the US dollar or US Treasury bonds, their Schwarzschild radius can be seen as the security of centralized entities. This centralized issue includes not only the stablecoins themselves, but also banks and custodian institutions. Although we all understand that both USDT and USDC have existed for so many years and have survived numerous FUDs, their history is only relatively long compared to the crypto world. No one can guarantee that there are any centralized institutions in the world that are too big to fail. After all, even Lehman Brothers could go bankrupt. Once there is a situation of losing collateral or being unable to convert back to US dollars (USDC also almost encountered this crisis in March this year), they will be instantly run on and become “black holes”.

Looking back at the history of currency in the real world, these mechanisms have actually collapsed into black holes. For example, the collapse of the gold standard was due to the imbalance of gold reserves during the war and the central banks printing a large amount of money. The gold reserves could not match the total amount of money printed, and the common people had no idea how much gold reserves the banks actually had. Only when a run occurs do people realize that the money in their hands is already worthless, and in the end, excessive money printing by central banks became a legitimate thing (modern fiat currency system). As for the situation of pegging one currency to another, such as the indirect pegging of the British pound to the German mark, Britain briefly participated in the European Exchange Rate Mechanism (ERM), which is a semi-fixed exchange rate system among multiple currencies. In the ERM, the exchange rates of participating countries fluctuated within a relatively narrow range, and the German mark often served as an “anchor” currency. This can be seen as an indirect pegging. However, due to various factors (including the increase in interest rates caused by Germany’s reunification and the need to lower interest rates in the UK to stimulate exports due to domestic economic pressures), maintaining a fixed exchange rate in the ERM became increasingly unsustainable for Britain.

The famous Black Wednesday event in history happened at this moment. Soros discovered the vulnerability in this system, and together with some long-term speculative funds and multinational companies, he shorted weak European currencies in the market, forcing these countries to spend a huge amount of money to stabilize their currency values.

On September 15, 1992, Soros decided to heavily short the pound, and the pound fell all the way to 2.8 against the mark. At this point, the pound was on the edge of exiting the European Exchange Rate Mechanism (ERM). On the 16th, even though the UK Chancellor of the Exchequer raised the country’s interest rate to 15% within a day, the effect was minimal. In this battle to defend the pound, the UK government used $26.9 billion of foreign exchange reserves, and the central bank repurchased £2 billion every hour, but still couldn’t keep the exchange rate above the minimum of 2.778. In the end, they suffered a devastating defeat and were forced to exit the ERM. Soros made nearly $1 billion in profits from this battle and became famous overnight. The method of shorting LUNA is almost identical to this.

Credit Money

The modern monetary system is built on the credit of centralized governments. The money in our hands is debt from banks or governments, and government bonds are debts of debts. Modern money is essentially “credit money.” The constant issuance of government debt only devalues the currency and accelerates the cycle of inflation. This monetary system may be the largest Ponzi scheme in human history. However, when it comes to “money,” most people do not think of anything other than fiat currency. This is because people have accepted this Schelling point, where a scam lasts long enough to be considered “real.” To establish a stablecoin on the blockchain, we may have to accept a certain level of Ponzi existence.

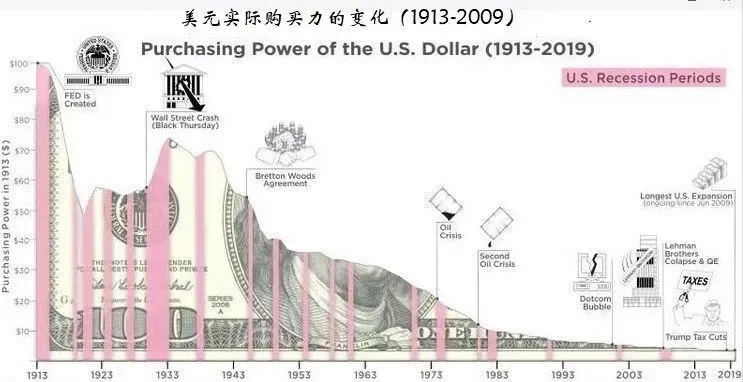
Changes in the purchasing power of the US dollar (Source: Tencent News)

Reflection

So, here are my personal views on how to establish a currency on the blockchain:

– Low volatility but allows for fluctuations, with sufficient liquidity;

– Not forcibly pegged to any fiat currency;

– Allocations based on supply and demand indicators;

– Acceptance of a certain level of Ponzi existence, making this currency a Schelling point;

– Sufficient number of use cases, capable of bridging the gap to real-world payments.

Floating Stablecoin, f(x) Protocol

f(x) is an ETH leveraged protocol designed to meet the demand for stable assets in the cryptocurrency field while mitigating centralized risks and capital efficiency problems. The f(x) protocol introduces a new concept called “floating stablecoin” or fETH. fETH is not pegged to a fixed value but instead gains or loses a small portion of the price changes in native Ethereum (ETH). In addition, a supplementary asset called xETH is created, which acts as a zero-cost leveraged long ETH position. xETH absorbs most of the volatility in ETH price changes, stabilizing the value of fETH.

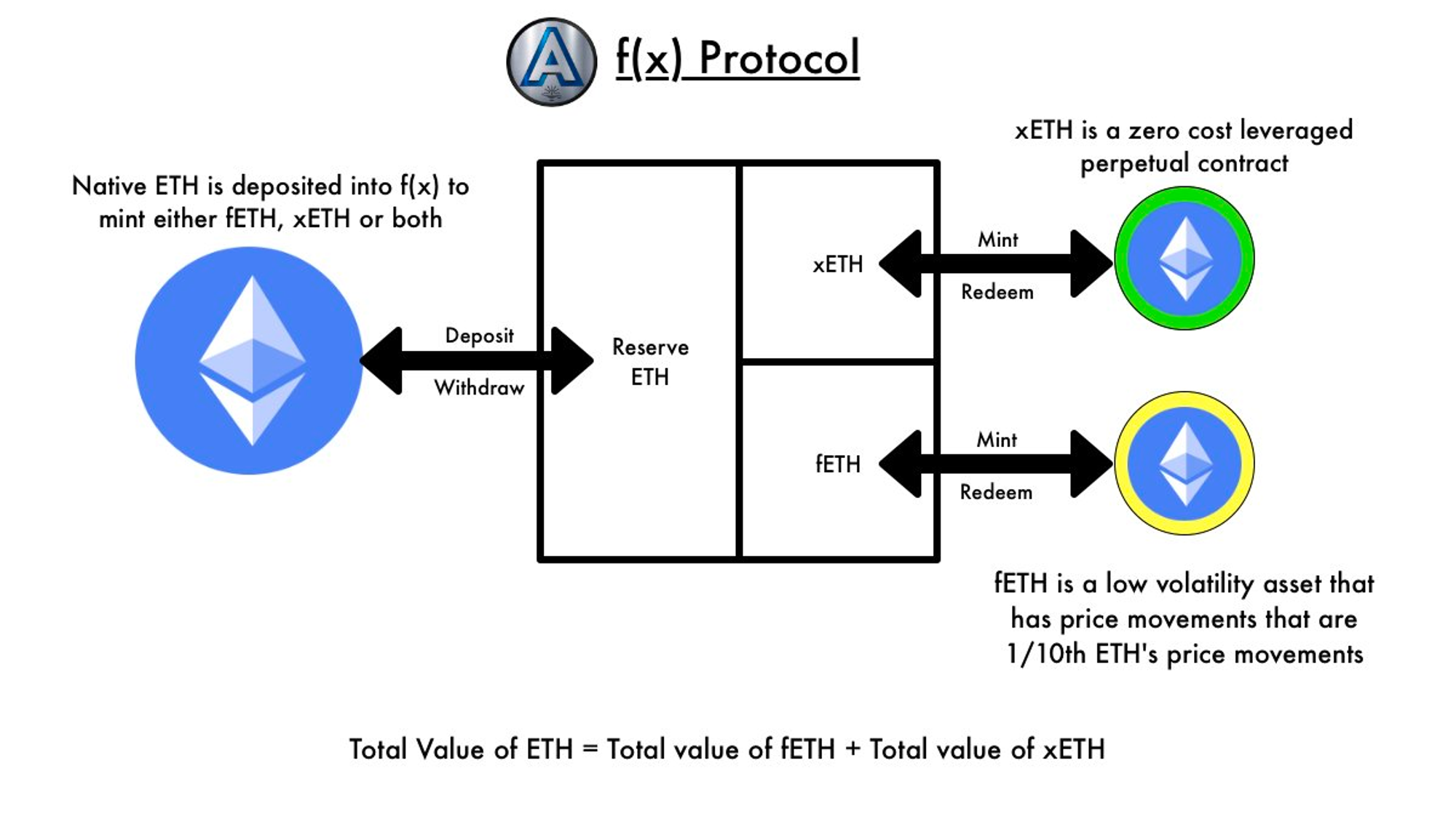
Source: f(x) Official X

·fETH: Low volatility ETH asset, with a price that fluctuates 1/10th of the native ETH price (β coefficient of 0.1). For example, if today’s ETH price is $1650, the minted fETH will be 1650, with a price of $1650. If tomorrow’s ETH price drops to $1485, the price of fETH will still be maintained at $1633.5, and vice versa. You can also think of it as 90% stablecoin + 10% ETH;

·xETH: Zero-cost leveraged long ETH position, used to absorb the volatility of ETH and stabilize the price of fETH (i.e., β> 1). These xETH can be traded in DeFi (supported by the demand for long ETH positions).

The β coefficient can be adjusted in this mechanism.

β

In finance, Beta is a measure that quantifies the volatility of an asset or portfolio relative to the overall market. It is a key parameter in the Capital Asset Pricing Model (CAPM), used to estimate the expected return and risk of an asset.

Calculation Method

Beta is calculated through regression analysis, usually by comparing the returns of individual assets with the returns of the overall market (usually represented by market indices such as the S&P 500). Mathematically, Beta is the slope in the regression equation:

Asset Return = α + β × Market Return

Where α is the intercept term, representing the expected return of the asset in a risk-free scenario, and β is the slope, representing the sensitivity of the asset to market returns.

Explanation

·β = 1: The volatility of the asset is consistent with the overall market volatility;

·β > 1: The asset is more volatile relative to the market, meaning it may have larger fluctuations when the market rises or falls;

·β < 1: The asset is relatively stable compared to the market, with smaller volatility;

·β = 0: There is no correlation between the asset and market returns, typically representing risk-free assets such as government bonds;

·β < 0: The asset is negatively correlated with market returns, meaning it may have positive returns when the market declines, thus serving as a hedge.

Working Principle

The f(x) protocol only accepts ETH as collateral and supports low and/or high volatility (β) tokens backed by that collateral. Providing ETH allows users to mint fETH and/or xETH, with the quantity based on the price of ETH and the current Net Asset Value (NAV) of each token. Conversely, users can redeem fETH or xETH for NAV ETH from the reserves at any time.

The NAV of fETH and xETH changes with the price of ETH, so at any given time, the total value of all fETH plus the total value of all xETH equals the total value of the ETH reserve. In this way, each fETH and xETH token has its NAV support and can be redeemed at any time. Mathematically, the invariant holds at all times:

In the formula, neth represents the quantity of ETH collateral, peth represents the ETH USD price, nf represents the total supply of ETH, pf represents the ETH NAV, nx represents the total supply of xETH, and px represents the xETH NAV.

This protocol adjusts its NAV based on the changes in ETH price to limit the volatility of fETH, so that the 10% return of ETH (for βf=0.1) is reflected in the fETH price. The protocol also adjusts the xETH NAV to exceed the return of ETH in order to maintain the invariance of f(x) (Equation 1). In this way, xETH provides leveraged ETH returns (tokenized, zero financing cost), while fETH shows low volatility, and both remain decentralized and trustworthy.

Risk Model

In fact, under this concept, fETH relies on the existence of xETH. If the demand for xETH is not large enough, the 0.1β coefficient of fETH cannot be maintained, or if the volatility is too high, the protocol introduces a CR formula to calculate the health level of the entire system.

CR is the total collateral value divided by the total NAV of fETH, and four risk levels are set based on the percentage.

If the CR of the system drops to a risk level that cannot maintain the ability of βf=0.1, the risk management system of the system will initiate four progressively stronger modes to guide the system back to overcollateralization. Each mode sets a CR threshold, and when it is lower than the threshold, additional measures will be initiated to help maintain the stability of the entire system. As long as the CR is below its specified level, the incentives, fees, and controls described in each mode will remain effective. For example, if Level 3 is effective, it means that Level 1 and Level 2 are also effective. When the CR recovers to the relevant level, they will automatically resume.

·Level 1——Stability Mode: When the CR value is below 130%, the system enters stability mode. In this mode, fETH minting is disabled, and the redemption fee is set to zero. The redemption fee for xETH is increased, and xETH miners receive additional rewards in the form of small stability fees from fETH holders;

·Level 2——User Rebalance Mode: When the CR value is below 120%, the system enters user rebalance mode. In this mode, users can earn rewards by exchanging fETH for ETH, and the remaining fETH holders pay stability fees in a similar manner to stability mode. In this way, users can earn slightly more returns than the NAV of fETH when redeeming. In this mode, the redemption fee for fETH is set to zero;

·Level 3——Agreement Balance Mode Again: When the CR value is below 114%, the system enters the agreement rebalance mode again. This mode is similar to Level 2, except that the protocol itself can use reserves for rebalancing. This mode is unlikely to be triggered because the rebalancing actions of Level 2 are profitable, and user response is faster than the protocol. However, it creates an additional layer of protection. In this mode, the protocol uses ETH from the fETH reserves to purchase on the market and then burn fETH from the AMM. Using this mechanism, the NAV of fETH will only decrease by the rebalancing stability fees obtained by the protocol in this case;

·Level 4——Recapitalization: In the most extreme cases, the protocol has the ability to issue governance tokens to raise ETH for capital restructuring through the minting of xETH or the purchase and redemption of fETH.

Conclusion

The f(x) Protocol proposes an interesting method of creating stablecoins by controlling volatility. However, it still has some noticeable drawbacks, as fETH can only exist in relatively stable market conditions and when xETH adopts a sufficiently high level. But it is indeed a very innovative idea. It is inevitable that blockchain will fail to establish a system similar to modern credit currency under the premise of decentralization (it can only potentially succeed in a centralized situation). Therefore, we need to focus on sufficient application scenarios and low volatility with liquidity. Personally, I believe that some meme tokens (such as Dogecoin) have the potential to develop application scenarios, and there are also other attempts besides f(x) in terms of stability. For something in its infancy, we should have patience and tolerance.

References

1. f(x) Whitepaper

2. Terra Money: Stability and Adoption

3. The Decentralization of Currency

4. The Lord of Algorithmic Stablecoins: After LUNA, There Will Be No More UST

5. Unveiling the LUNA Coin: Why I Believe the Attempt of Algorithmic Stablecoins is Doomed to Fail

Like what you're reading? Subscribe to our top stories.

We will continue to update Gambling Chain; if you have any questions or suggestions, please contact us!

Gambling Chain