Author: Steven Yue, originally published on the author’s Zhihu
In the previous article, we learned about the definition and specific stages of Fully Homomorphic Encryption (FHE), and also reviewed the history of FHE. At this point, everyone should have a preliminary understanding of FHE system. (You can click on “A Preliminary Exploration of Fully Homomorphic Encryption: Definition and Historical Review” to view the original article)
In the previous article, we mentioned the GSW system, which is the third-generation Fully Homomorphic Encryption system we talked about. The construction of the GSW system is mainly based on the well-known Learning With Errors (LWE) problem in lattice cryptography. In order to better understand the specific construction of the GSW system, we will quickly learn about lattice cryptography and the LWE problem in this article.
Lattice-based cryptography is a popular branch of cryptography that has the property of resisting quantum computing. In the upcoming NIST post-quantum era encryption algorithm standardization discussion, lattice-based encryption systems are one of the choices. However, don’t be intimidated by these definitions. In fact, understanding lattice cryptography is very simple, we just need some basic knowledge of linear algebra.
- How will the design centered around intent affect the blockchain system?
- Investors pay attention to how the Hong Kong government regulates exchange compliance from the perspective of JPEX’s scandal.
- The first Ethereum Hong Kong event is about to arrive, heavyweight guests including Vitalik Buterin will appear at ETH Hong Kong.
PS: If you are not familiar with linear algebra, I strongly recommend watching the video collection “Essence of Linear Algebra” by the great master 3Blue1Brown. The videos vividly describe the basic theorems of linear algebra.
A Quick Introduction to Lattice Cryptography
What exactly is lattice cryptography? After listening for a while, I believe many of you still haven’t figured it out. In fact, lattice cryptography is a set of cryptographic systems defined based on lattices and some problems on lattices. So we need to first understand what a lattice is.
To give a more convenient example, let’s introduce the simplest lattice system here – the integer lattice.
Construction of the Integer Lattice






PS: There is another difficult problem in lattice cryptography called the Shortest Vector Problem (SVP), which is different from CVP but also an NP-hard problem. We won’t explain it in detail here.

Learning With Error (LWE) Problem
At this point, I believe everyone should have a rough understanding of the integer lattice and also know about a difficult problem in the integer lattice: the CVP problem. Now let’s take a look at how we can derive our main character, the LWE problem, from the CVP problem. To better understand LWE, let’s start by reviewing some middle school mathematics~
In middle school or high school math classes, we should have learned how to solve systems of linear equations. Generally, we are given a set of linear equations:


Gaussian Elimination with Noise
Once we learn how to solve linear equations, we find that it is not a difficult problem. We just need to constantly use Gaussian elimination between rows to obtain the solution of the unknown variables. After all, this is a math problem we learned in middle school, not that difficult.
Now, let’s add some difficulty to this Gaussian elimination problem: add noise.







Dlog Problem in Diffie-Hellman Public Key Exchange
At this point, friends familiar with cryptography may not be unfamiliar with multiple versions of a problem (such as search, decision, etc.). Yes, when we learn about the Diffie-Hellman public key exchange problem, we also use the same problem transformation. If friends who are not familiar with it are not in a hurry, let me explain it.



Comparison of Difficulty between DLWE and DDH
Why do we have to talk so much about the DDH problem? This is because, after understanding the difficulty of SLWE/DLWE and CDH/DDH in the field of cryptography, we can compare the distribution of their difficulty levels.
The DDH assumption is actually very imperfect, even headache-inducing. Because of the existence of the LianGuaiiring backdoor, this directly sets an astonishing lower limit for the difficulty of the DDH problem – it is too easy in groups where LianGuaiiring exists. Therefore, when selecting a group, we must choose carefully. The elder brother CDH of DDH is different because there is no efficient algorithm to crack the discrete logarithm, so the complexity in any cyclic group is relatively average. In this way, even if CDH is difficult, it does not provide much substantial help in the distribution of the difficulty of DDH. We often need to use average difficulty to define the difficulty of the DDH problem (because the lower limit is too low). This is a very frustrating thing in cryptography, just like giving you a car but telling you that there is a certain possibility that the car will fall apart as soon as you drive it.
Compared to LWE, the problem of DLWE is much more perfect. Because there is no backdoor like LianGuaiiring, the difficulty of DLWE is actually the same as SLWE. Whether it is solving DLWE or SLWE, we will be stuck at the step of how to restore the unknown vector S. Problems of this kind, even if the problem form is transformed, but the complexity guarantees roughly the same problem, are rare treasures in cryptography. For the difficulty of DLWE, we can elegantly define it using Worst Case Performance.
This paragraph is actually somewhat of a sentiment for everyone in the cryptography community. Having a clean definition is much more comfortable than dealing with a bunch of messy assumptions. This is also why lattice cryptography is so attractive. However, these little emotions about difficulty/complexity are irrelevant to our understanding of fully homomorphic encryption. You can treat them as interesting trivia, just take a look.
Practical Application of DLWE: Lattice Cryptography and the Regev Encryption Algorithm
If you have successfully chewed through the previous content and have made it to this point, congratulations! Now you have mastered the basics of LWE and lattice cryptography!
Now that we have learned so much knowledge, let’s combine what we have learned before and take a look at how to use the LWE problem to construct a common public key encryption system in lattice cryptography – the Regev encryption algorithm.
Regev encryption is an encryption system invented by a genius named Regev in 2005. It is a public key encryption system very similar to the ElGamal type, based on the assumption of DLWE. Let’s take a look at its specific definition:




Security of Regev Encryption
Just now, we digressed from the topic of discussion. Now let’s continue to learn about the security of the Regev encryption system.
In order to prove that the Regev encryption scheme is semantically secure, we need to use a common proof tool in cryptography: the hybrid argument. The hybrid argument is not some black technology, but rather a way of dividing the problem to be proven into several small steps, and then proving them step by step.
First, let’s take a look at what the worldview of a third party who eavesdrops on all the encrypted messages of the Regev encryption system would be like:

Next, we can create a second similar worldview:
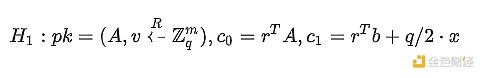


To Be Continued: Building Limited-level Fully Homomorphic Algorithm
Finally, let’s review the content of this issue~
First, we saw the definition of Integer Lattice and then based on it, we understood the NP-hard problem of Closest Vector Problem (CVP). Afterwards, we reviewed the problem of solving systems of linear equations that we learned in high school and unified it as the Gaussian elimination problem. Next, we added a random error noise to the Gaussian elimination problem itself, forming our main character, the Learning with Errors (LWE) problem.
After understanding what LWE is, we studied the formal definition of the LWE problem in detail, as well as the parameters n, m, q, and B. Then we transformed the Search LWE (SLWE) into the Decision LWE (DLWE) problem, and discussed why the assumptions of SLWE/DLWE are better than CDH/DDH. Finally, combining all the knowledge we learned, we built the classic Regev encryption algorithm in lattice cryptography, encrypting a ciphertext (a bit) based on the hardness assumption of LWE.
If you have read this far and successfully understood all the content, then you have actually mastered 80% of the essence of fully homomorphic encryption! Next, all we need to do is to put these parts together like building blocks to construct the fully homomorphic encryption system we want.
Due to the length, this issue ends here. In the next issue, we will use the knowledge learned in this issue to build a limited-level fully homomorphic encryption system together.
Like what you're reading? Subscribe to our top stories.
We will continue to update Gambling Chain; if you have any questions or suggestions, please contact us!