Explaining BIP 158 Compact Block Filters

Author: Elle Mouton

In this article, I will briefly introduce the need for Bitcoin light clients, and why “compact block filters” are better than “Bloom filters” in meeting this need. Then, I will explain in depth how compact block filters work, and provide a step-by-step guide for constructing such a filter on a testnet.

The significance of block filters

Bitcoin light clients are a type of software that aims to support Bitcoin wallets without storing the Bitcoin blockchain. This means that it needs to be able to broadcast transactions to the network, but most importantly, it must be able to find new transactions related to the wallet from the chain. There are two types of related transactions: sending funds to the wallet (creating a new output for an address in the wallet) and spending one of the UTXOs controlled by the wallet.

• Polygon shares its Polygon 2.0 architecture, which consists of Staking Layer, Interoperability Layer, Execution Layer, and Proof-of-Stake Layer.
• Quick Overview of Ethereum Scaling Solutions Evolution: OP Stack, Arbitrum Orbit, Polygon 2.0…
• Analysis and Summary of Initial Token Distribution Method for Buidler DAO

What’s wrong with Bloom filters?

Before the emergence of BIP 158, the most commonly used method for light clients was the Bloom filter described by BIP 37. The pattern of a Bloom filter is that you find all the data objects you are interested in (such as spent and created UTXO script public keys), hash them multiple times one by one, and then add each result to a bit map called a “Bloom filter”. This filter represents what you are interested in. Then, you send this filter to a Bitcoin node you trust and ask them to send you everything that matches this filter.

The problem is that this process is not very private, because you are still leaking some information to the Bitcoin nodes receiving the filter. They can know the transactions you are interested in as well as the transactions you are not interested in at all; they can also choose not to send you anything that matches the filter. So this is not ideal for light clients. However, it is not ideal for Bitcoin nodes that provide services to light clients either. Every time you send a filter, they must load the relevant blocks from the hard disk and determine if there are any transactions that match your filter. By simply sending fake filters continuously, you can bombard them – this is essentially a DOS attack. It only takes very little energy to create a filter, but it takes a lot of energy to respond to such requests.

Compact Block Filters

OK, so the properties we’re looking for are:

• Stronger privacy

• Less asymmetric client-server load. That is, the server should do less work.

• Less trust. Light clients shouldn’t have to worry about the server omitting relevant transactions.

With compact block filters, the server (full node) constructs a deterministic filter for each block that includes all data objects in that block. This filter is calculated once and can be saved permanently. If a light client requests a filter for a particular block, there is no asymmetry here – the server doesn’t need to do more work than the client that initiated the request. Light clients can also choose multiple sources of information to download full blocks from to ensure they are consistent, and, in any case, light clients can always download full blocks to check if the filters provided by the server are correct (matching the relevant block content). Another benefit is that this way is more private. Light clients no longer need to send the server fingerprints of the data they want. Analyzing a light client’s activity also becomes more difficult. After obtaining such filters from the server, the light client checks whether the filter contains the data they want. If it does, the light client requests the full block. It should be noted that to serve light clients in this way, full nodes need to persistently save these filters, and light clients may also want to persistently save a few filters, so it is important to keep the filters as lightweight as possible (which is why it’s called “compact block filters”).

Great! Now we’re getting to the good stuff. How are these filters created? What do they look like?

Our requirements are:

• We want to put the fingerprints of specific objects in the filter so that when a client wants to check whether a block might contain content relevant to itself, they can list all the objects and check whether a filter matches these objects.

• We want the filter to be as small as possible.

• Essentially, what we want is something that can summarize some information about a block with a volume far smaller than the block itself.

The basic information contained in the filter includes the public key script for each transaction input (i.e., the public key script for each spent UTXO) and the public key script for each output in each transaction. It looks something like this:

objects = {spk1, spk2, spk3, spk4, ..., spkN} // a list of N script public keys

Technically, we can stop here — this list of script public keys can serve as our filter. This is a condensed version of a block that contains the information needed by a light client. With such a list, a light client can 100% confirm whether a block contains a transaction of interest. However, this list is very large. So, all our subsequent steps are geared toward making this list as compact as possible. This is where things get interesting.

First, we can convert each object to a number within a certain range and make each object number uniformly distributed within that range. Let us say we have 10 objects (N = 10), and we have a function that can convert each object to a number. Let us say we choose a range of [0, 10] (because we have 10 objects). Now, our “hash and convert to a number” function will take each object as input and produce a number between 0 and 10, inclusive. These numbers are uniformly distributed within this range. This means that after sorting, we get a graph that looks like this (in an idealized case):

First of all, this is great because we have greatly reduced the size of each object’s fingerprint. Now each object is just a number. So, our new filter looks like this:

numbers := {1,2,3,4,5,6,7,8,9,10}

A light client downloads this filter and wants to know whether an object of interest matches this filter. They simply take the object of interest, run the same “hash and convert to a number” function, and see whether the result matches any of the numbers in the filter. So, what’s the problem? The problem is that the numbers in the filter already occupy all the possibilities within this space! This means that no matter what kind of object the light client is interested in, the resulting number is always going to match the filter. In other words, the “false positive rate” of this filter is 1. This is not good. It also means that we have lost too much information in the process of compressing the data to generate the filter. We need a higher false positive rate. So, let’s say we want a false positive rate of 5. Then we can evenly distribute the objects in the block to numbers in the range [0, 50]:

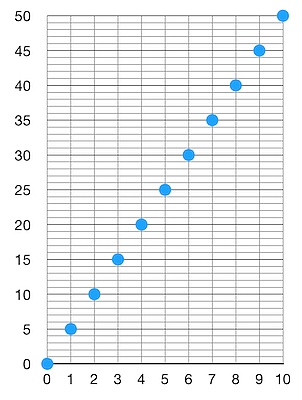
This looks much better. If I were a client and downloaded such a filter, the probability of false positives (the filter indicating that an object of interest is in the corresponding block when it is not) would decrease to 1/5 when checking whether an object of interest is in the corresponding block through the filter. Great! Now we have mapped 10 objects to numbers ranging from 0 to 50. This new list of numbers is our filter. Again, we can stop here, but we can also compress it further!

Now we have an ordered list of numbers that are evenly distributed in the range [0, 50]. We know that there are 10 numbers in this list. This means that we can infer that the most likely difference between two adjacent numbers in the ordered list is 5. In general, if we have N objects and want a false positive rate of M, the size of the space should be N * M. That is, the size of these numbers should be between 0 and N * M, but the difference between adjacent numbers (after sorting) should be M with high probability. Storing M requires less space than storing N * M. Therefore, we do not need to store every number, we can store the difference between adjacent numbers. In the example above, this means that we store [0, 5, 5, 5, 5, 5, 5, 5, 5, 5] instead of [0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50], and it is easy to reconstruct the initial list from this. If you compress it further, storing the number 50 obviously takes up more space than storing the number 5. But why stop there? Let’s compress it even more!

Next, we will use “Golomb-Rice encoding”. This encoding method can encode a list in which each number in the table is very close to a certain number very well. And our list is just like that! Each number in our list is likely to be close to 5 (or close to our false positive rate, M), so taking the quotient of each number and M (dividing each number by 5 and ignoring the remainder) is likely to be 0 (if the number is slightly less than 5) or 1 (if the number is slightly greater than 5). The quotient may also be 2, 3, etc., but the probability is much smaller. Great! So we can use this: we use as few bits as possible to encode smaller quotients, and use more bits to encode larger but less likely quotients. Then, we also need to encode the remainder (because we want to be able to accurately rebuild the entire list), and these remainders are always in the range [0, M-1] (in this case, [0, 4]). To encode the quotient, we use the following mapping:

The above mapping is easy to understand: the quantity of the number 1 represents the quotient we want to encode, while 0 represents the end of the quotient encoding. So for each number in our list, we can use the above table to encode the quotient, and then convert the remainder to binary using a bitstream that can represent a maximum value of M-1. Here, the remainder is 4, so we only need 3 bits. Here is a table showing the possible remainders and their encodings in our example:

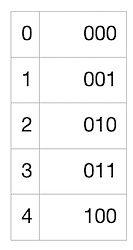
So, in an ideal scenario, our list [0, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5] can be encoded as:

0000 10000 10000 10000 10000 10000 10000 10000 10000 10000

Before we move on to a more realistic scenario, let’s see if we can recover our original list from this filter.

Now we have “0000100001000010000100001000010000100001000010000”. We know about Golomb-Rice encoding and we know that M is 5 (because this will be public knowledge and anyone constructing a filter using this method will know it). Because we know that M is 5, we know there will be 3 bits to encode the remainder. So we can turn this filter into the following “quotient-remainder” array list:

[(0, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0), (1, 0)]

Knowing that the quotient is obtained by dividing by M (5), we can recover:

[0, 5, 5, 5, 5, 5, 5, 5, 5, 5]

And since we know that the list represents the difference between adjacent numbers, we can recover the original list:

[0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50]

A More Realistic Example

We are now going to attempt to construct a filter for a real Bitcoin testnet block. I will be using block 2101914. Let’s see what its filter looks like:

$ bitcoin-cli getblockhash 2101914000000000000002c06f9afaf2b2b066d4f814ff60cfbc4df55840975a00e035c$ bitcoin-cli getblockfilter 000000000000002c06f9afaf2b2b066d4f814ff60cfbc4df55840975a00e035c{  "filter": "5571d126b85aa79c9de56d55995aa292de0484b830680a735793a8c2260113148421279906f800c3b8c94ff37681fb1fd230482518c52df57437864023833f2f801639692646ddcd7976ae4f2e2a1ef58c79b3aed6a705415255e362581692831374a5e5e70d5501cdc0a52095206a15cd2eb98ac980c22466e6945a65a5b0b0c5b32aa1e0cda2545da2c4345e049b614fcad80b9dc9c903788163822f4361bbb8755b79c276b1cf7952148de1e5ee0a92f6d70c4f522aa6877558f62b34b56ade12fa2e61023abf3e570937bf379722bc1b0dc06ffa1c5835bb651b9346a270",  "header": "8d0cd8353342930209ac7027be150e679bbc7c65cc62bb8392968e43a6ea3bfe"}

Alright dear, let’s see how we construct such a filter from blocks. The complete code used here can be found in this github repository. Here I will only show some pseudo-code fragments. The core of this code is a function called constructFilter, which the Bitcoin client can use to call bitcoind and the corresponding block. This function looks like this:

func constructFilter(bc *bitcoind.Bitcoind, block bitcoind.Block) ([]byte, error) {    // 1. Collect all the objects we want to add to a filter from the block    // 2. Convert these objects to numbers and sort them    // 3. Get the difference between adjacent numbers in the sorted number list    // 4. Use Golomb-Rice encoding to encode these differences}

So, the first step is to collect all the objects we want to add to the filter from the block. Starting from BIP, we know that these objects include all spent script public keys and script public keys for every output. BIP also sets some additional rules: we will skip inputs of coinbase transactions (because it doesn’t make sense as it has no input), and we will skip all OP_RETURN outputs. We will also remove duplicate data. If there are two identical script public keys, we will only add them to the filter once.

// The list of objects we want to add to the filter// Includes all spent script public keys and script public keys for every output// We use a "map" to remove duplicate script public keysobjects := make(map[string] struct{})// Traverse every transaction in the blockfor i, tx := range block.Tx {        // Add the script public key for every output// to our object list        for _, txOut := range tx.Vout {                scriptPubKey := txOut.ScriptPubKey                if len(scriptPubKey) == 0 {                        continue                }                // Skip over OP_RETURN (0x6a) outputs                if spk[0] == 0x6a {                        continue                }                objects[skpStr] = struct{}{}        }        // Do not add inputs of the coinbase transaction        if i == 0 {                continue        }        // For each input, get its script public key        for _, txIn := range tx.Vin {                prevTx, err := bc.GetRawTransaction(txIn.Txid)                if err != nil {                        return nil, err                }                scriptPubKey := prevTx.Vout[txIn.Vout].ScriptPubKey                if len(scriptPubKey) == 0 {                        continue                }                objects[spkStr] = struct{}{}        }}

OK, we have collected all of the objects. Next, we define the variable N as the length of the object graph. Here, N is 85.

The next step is to convert our objects into numbers uniformly distributed within a range. Again, this range depends on how high of a false positive rate you want. BIP158 defines the constant M as 784931. This means that the probability of a false positive is 1/784931. As we did before, we take the false positive rate M multiplied by N to get the range of all the numbers. We define this range as F, that is F = M * N. Here, F is 66719135. I’m not going to go into detail on the function that maps objects to numbers (you can find the relevant details in the linked github repository above). What you need to know is that it takes the object, the constant F (defining the range to which objects should be mapped), and a key (block hash value) as input. Once we have all the numbers, we’ll sort this list in ascending order, and then create a new list called differences, which saves the difference between adjacent numbers in the sorted number list.

numbers := make([]uint64, 0, N)// Iterate over all objects, convert them to a number uniformly distributed in the [0, F] range, // and store these numbers as the `numbers` listfor o := range objects {        // Using the given key, max number (F) and object bytes (o),        // convert the object to a number between 0 and F.        v := convertToNumber(b, F, key)        numbers = append(numbers, v)}// Sort the list of numbers.sort.Slice(numbers, func(i, j int) bool { return numbers[i] < numbers[j] })// Convert the list of numbers to a list of differencesdifferences := make([]uint64, N)for i, num := range numbers {        if i == 0 {                differences[i] = num                continue        }        differences[i] = num - numbers[i-1]}

Great! Here is a picture showing the numbers and differences lists.

As you can see, the 85 numbers are evenly distributed throughout the entire space! So the values in the differences list are also very small.

The final step is to use Golomb-Rice encoding to encode this differences list. Recall from earlier explanations that we need to divide each difference by the most likely value, then encode the quotient and remainder. In our earlier example, I said the most likely value is M, and the remainder will be in [0, M]. However, BIP158 does not do it this way, because we found that 2, which is not actually a parameter that minimizes the final filter volume. So we don’t use M, but define a new constant P, and use 2 ^ P as the Golomb-Rice parameter. P is defined as 19. This means that we need to divide each difference by 2 ^ 19 to get the quotient and remainder, and the remainder will be encoded in 19 bits in binary.

filter := bstream.NewBStreamWriter(0)// For each value in the `differences` list, obtain the quotient and remainder by dividing by 2 ^ P.for _, d := range differences {        q := math.Floor(float64(d)/math.Exp2(float64(P)))        r := d - uint64(math.Exp2(float64(P))*q)        // Encode the quotient        for i := 0; i < int(q); i++ {               filter.WriteBit(true)        }        filter.WriteBit(false)        filter.WriteBits(r, P)}

Great! Now we can output the filter and get:

71d126b85aa79c9de56d55995aa292de0484b830680a735793a8c2260113148421279906f800c3b8c94ff37681fb1fd230482518c52df57437864023833f2f801639692646ddcd7976ae4f2e2a1ef58c79b3aed6a705415255e362581692831374a5e5e70d5501cdc0a52095206a15cd2eb98ac980c22466e6945a65a5b0b0c5b32aa1e0cda2545da2c4345e049b614fcad80b9dc9c903788163822f4361bbb8755b79c276b1cf7952148de1e5ee0a92f6d70c4f522aa6877558f62b34b56ade12fa2e61023abf3e570937bf379722bc1b0dc06ffa1c5835bb651b9346a270

Other than the first two bytes, the rest is exactly the same as the filter we obtained in bitcoind! Why are the first 2 bytes different? Because the BIP says that the value of N needs to be encoded in the VarInt format and appear at the beginning of the filter so that the receiver can decode it. This is accomplished with the following code:

fd := filter.Bytes()var buffer bytes.Bufferbuffer.Grow(wire.VarIntSerializeSize(uint64(N)) + len(fd))err = wire.WriteVarInt(&buffer, 0, uint64(N))if err != nil {        return nil, err}_, err = buffer.Write(fd)if err != nil {        return nil, err}

If we print the filter now, we will see that it is exactly the same as the result from bitcoind:

5571d126b85aa79c9de56d55995aa292de0484b830680a735793a8c2260113148421279906f800c3b8c94ff37681fb1fd230482518c52df57437864023833f2f801639692646ddcd7976ae4f2e2a1ef58c79b3aed6a705415255e362581692831374a5e5e70d5501cdc0a52095206a15cd2eb98ac980c22466e6945a65a5b0b0c5b32aa1e0cda2545da2c4345e049b614fcad80b9dc9c903788163822f4361bbb8755b79c276b1cf7952148de1e5ee0a92f6d70c4f522aa6877558f62b34b56ade12fa2e61023abf3e570937bf379722bc1b0dc06ffa1c5835bb651b9346a270

Success! However, my personal understanding is that it is not necessary to include N in the filter. If you know the value of P, then you can find the value of N. Let’s see if we can use the first filter to output the initial list of numbers:

b := bstream.NewBStreamReader(filter)var (    numbers []uint64    prevNum uint64)for {        // Read quotient from the byte string. The first 0 encountered indicates the end of the quotient        // The number of 1s encountered before the next 0 indicates the quotient        var q uint64        c, err := b.ReadBit()        if err != nil {                return err        }        for c {                q++                c, err = b.ReadBit()                if errors.Is(err, io.EOF) {                        break                } else if err != nil {                        return err                }        }        // The next P bits encode the remainder        r, err := b.ReadBits(P)        if errors.Is(err, io.EOF) {                break        } else if err != nil {                return err        }        n := q*uint64(math.Exp2(float64(P))) + r        num :=  n + prevNum        numbers = append(numbers, num)        prevNum = num}fmt.Println(numbers)

The above operation generates the same list of numbers, so we can refactor it without knowing N. So I’m not sure what the reason is for including N in the filter. If you know why N must be included, please let me know!

Thanks for reading!

We will continue to update Gambling Chain; if you have any questions or suggestions, please contact us!

Follow us on Twitter, Facebook, YouTube, and TikTok.